河合です。今年度は高校3年生の担任をしています。昨年の高3生が卒業して3ヶ月。私にとって初めて受験指導をした卒業生たちは、コロナ禍に負けず大学生活を謳歌しているのでしょうか。時々、彼女たちのことを思います。早いもので、もうすぐ7月ですね。さて、久しぶりに百人一筆を担当します。今回は「ロジカルシンキング」についてお話したいと思います。

生徒の皆さん、突然ですが…

自分たちが大人になったとき（或いは、大人になるにつれて）、どのような能力が要求されると思いますか？

人々のお役に立つために

誰かを守り支えていくために

自分らしく生きていくために

どんな能力が身についていれば、幸せな人生を送ることができるのでしょうか。色んな意見があると思いますが、私は「ロジカルシンキング」がその答えの一つであると思っています。少なくとも、私の周りで幸せを掴んでいる方々は、この能力に長けている方が多いように感じています。

社会に目を向けると、企業の採用試験、経営戦略の立案・プレゼンテーションなど、実に様々な場面でロジカルシンキング、すなわち論理的思考力が要求されることがわかります。

特に、社会で新しい価値を創造していくためには、多くの人を巻き込んで仕事を推進していく必要が出てきます。もちろん、日頃から周囲の方々と協力して積極的にコミュニケーションをとる姿勢が重要なのは言うまでもないのですが、どこかで必ず自分の意思をはっきりと伝え、「相手を説得する（納得させる）力」が必要となってくるのです。仕事に限定せずとも、「自分の進むべき道・人生の選択を間違えない力」の要素の一つとして、このロジカルシンキングを磨いておくことに十分意味はあるはずです。

私は普段は数学を教えていますが、授業や課題を通じて、よく「どんな考え方なの？」と生徒に尋ねます。質問にくる生徒にも、同じことを聞きます。
信愛生の皆さん、普段の授業や課題に取り組む際、「きちんと自分の頭で考え抜く」ことができているでしょうか。

難しい問題に直面したとき、問題の捉え方を変えたり、状況を整理してみてください。きっと、違う視界が開け、解けるようになる問題も多くなっていくハズです。思考から逃げないようにしてほしいです。これから、期末試験が始まりますが、ぜひとも「思考力」を磨きながら勉強してくださいね。

 

それでは、ここで有名なクイズを一つご紹介します。時間のあるとき、挑戦してみてください。

 

1935年オーストリアの物理学者エルヴィン・シュレーディンガー博士が発表した論文の中に、【シュレディンガーの猫】という思考実験があり、このクイズはそれを応用したものです。最初はかなり難しく感じるかもしれませんが、友だちやご家族と紙に書き出したりして、う～んと悩みながらでも考えてみてください。

★問題

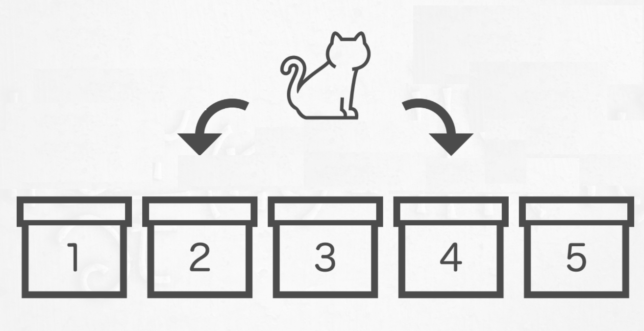
1〜5の番号が書かれた5つの箱があり、左から1,2,3,4,5の順で一列に並んでいる。この箱のどれか1つに猫が隠れている。猫は夜になると必ずひとつだけ隣の箱に移動する。朝になった時、飼い主は1つだけ箱を調べることができ、そこに猫がいるかどうか確認できる。飼い主は1週間以内に猫を見つけることができるだろうか？理由をつけて述べよ。

※ 以下、答えです

 

 

__________________________________________________________________________________________________________________________

★ 答え･ ･･ 「できる」　最適な行動により、遅くとも6日目には猫を発見することができる（以下、解説です）

この問題を解くカギは、「移動する猫」と「確認する飼い主」の非対称性にあります。
両者が移動・確認するのはともに「1つの箱」ですが、その選択肢には大きな差異が存在します。
猫が移動するのは「今いる場所の隣の箱」に限られますが、飼い主は「どの箱」でも調べられる。これが突破口になります。

 

・・・難しいですね。。。簡単な例で考えてみましょう！

【簡略化・具体化】「3つしか箱がない場合」

最適なのは、1日目に中央の「2」の箱を確認することです。もしここで猫が見つからない場合、猫は「1」「3」のどちらかの箱に隠れています。
なので、2日目も「2」の箱を確認すれば必ず猫を見つけることができますね。

「箱を調べたが猫はいなかった」ということに悲観的にならず、その事実そのものが、非常に大きな情報になります。このように考えると、最初から猫のいる位置を当てようとするのではなく、「猫がいる可能性のある箱」を少しずつ排除していくような戦略をとれば、最終的に必ず猫を見つけることができると捉えればよいのです。

生徒の皆さんは受験性複雑な問題に直面したとき、次のような3つの対処方法をもっておくと良いですよ。（数学の難題でも同様のアプローチが可能です）

➀簡略化・具体化
②仮定
③場合分け

➀によって、大抵何かしらのヒント・規則性が得られることができ、解決に近づきやすくなります。②で自分なりの仮説を立て、③であれこれ検証するといった感じです。

先ほどの➀の結果から、1日ごとに猫は必ず「偶数の箱」から「奇数の箱」へ、
あるいは「奇数の箱」から「偶数の箱」へ移動することがわかるので、箱の偶奇に注目して場合分けしてみましょう。

【仮説・場合分け】

・1日目に猫が「2」「4」の箱にいる場合

1日目：
「2」の箱を調べる。
「2」に猫がいる場合、ここで終了。
「2」に猫がいない場合、「4」に猫が隠れている。

2日目：
「3」の箱を調べる。
猫が「4」から「3」に移動した場合、ここで猫を発見。
しかし、猫が「4」から「5」に移動した場合、当然ですが猫は見つからない。

3日目：
「4」の箱を調べる。
2日目でも猫が見つからなかった場合、猫は必ず3日目には「4」の箱にいる。

これにて、猫を見つけることができました。

整理すると、猫が1日目に「2」「4」の箱に隠れている場合は、
「2」→「3」→「4」の順で箱を調べることで、遅くとも3日目には猫を発見できること判明。

・1日目に猫が「1」「3」「5」の箱にいる場合

2日目に猫は「2」「4」のどちらかにいることになります。ということは、
ここから先は、さっきの「猫が「2」「4」の箱にいる場合」と同じ戦略が使えるはず。

1日目「2」
2日目「3」
3日目「4」

の順で箱を調べて猫が見つからなかった場合、猫が1日目に隠れていたのは「1」「3」「5」のいずれか。
そして、この時点（3日目の朝の確認終了時）で猫が隠れているのも「1」「3」「5」のいずれかです。

ということは、4日目の朝、猫は「2」「4」のどちらかに隠れていることになる。ここから1〜3日目と同様に、4日目「2」 → 5日目「3」 → 6日目「4」と調べることで、遅くとも6日目には確実に猫を見つけることができる。

 

これが答えです。・・・文章にすると、わかりにくいかもしれませんね。ぜひ、表などを書いて視覚化し、思考の助けとすればよいでしょう。ぜひ、やってみてください。
__________________________________________________________________________________________________________________________