みなさんこんにちは。
吉田です。

今年の高3から大学入試共通テストに新たに「情報I」が課されることになっています。その目標に向けて、高3生は情報の勉強を頑張っております。
今回は、私が担当する情報の授業の様子を紹介します。

 

 

 

 

 

 

昨日はシミュレーションを行いました。

問題　銀行に100,000円預けて、年利0.4%で10年間預けるといくらになりますか。

これは教科書にある問題です。年利0.4%で固定されているので、確定的モデルと言われるものを作って解決します。

これは簡単ですね。これだけでは面白くないので、応用編として、熱烈な阪神ファンの頭取が経営する銀行で、阪神が優勝した翌年のみ年利をアップさせるという設定でもやってみました(詳細は下図)(実際、これに近い商品を出している銀行もあるようです)

 

 

 

 

 

 

 

 

 

 

 

 

 

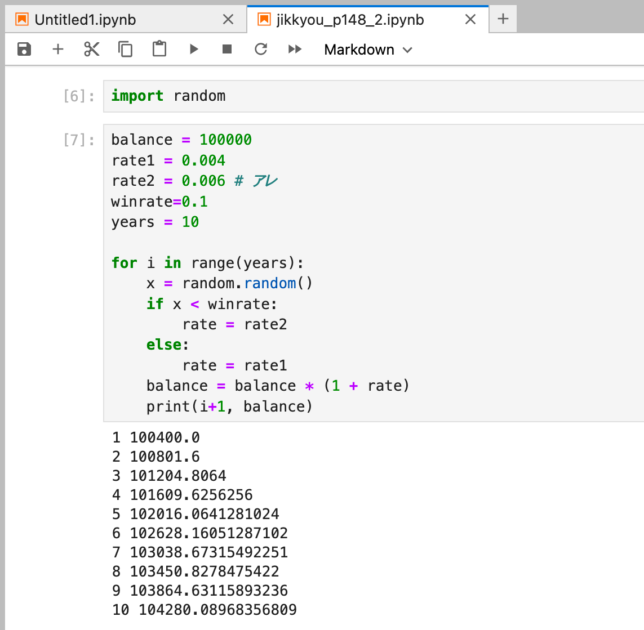
こちらは、阪神が優勝するかしないかが確率的に決まるので、確率的モデルを作ります。確定的モデルとは違い、実行するたびに結果が違ってきます。

次に、乱数を使って円周率πを求める方法も実施してみました。モンテカルロ法と言います。(詳細は下図)

 

 

 

 

 

 

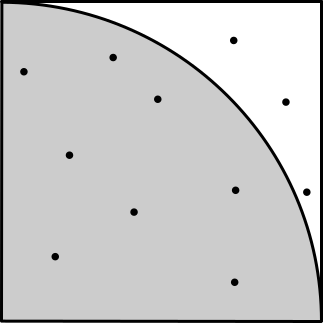
N=1000 ではπの正確な値は出てきませんが、N=100万くらいにしてみると、3.14… といったまぁまぁな値が得られます。

少し補足しておくと、πの値を求めるのにプロはこの方法は使いません。他にもっと精度の高い方法があるからです。モンテカルロ法の長所は(精度としては落ちるものの)難しい数学を使わないので、中学生程度の数学の知識で理解できるという点です。

蛇足ですがもう少し付け足しておくと、πの値を求める目的では使われないモンテカルロ法ですが、他の目的では使われます。手計算では解決できないような高次元の積分を数値積分(コンピュータを使って定積分を計算する方法)するときに使われるMCMC法というのがその一例で、物理の研究者たちには重宝されているようです。つまり、他にいい方法があるならそちらに譲るけど、他に方法がないときに次善の策として重宝されるのがモンテカルロ法だということです。